베르누이 방정식 정리
베르누이 방정식을 정리하겠습니다.
1. 베르누이정리란?
유체가 흐르는 속도와 압력, 높이의 관계를 수량적으로 나타낸 법칙이다.
(유체의 위치에너지와 운동에너지의 합이 항상 일정하다는 성질을 이용한 것)
유체역학의 기본 법칙 중 하나이며, 1738년 D. 베르누이가 발표하였다.
점성과 압축성이 없는 이상적인 유체가 규칙적으로 흐르는 경우에 대해
속력과 압력, 높이의 관계에 대한 법칙이다.
(유체의 위치에너지와 운동에너지의 합이 일정하다는 법칙에서 유도함.)

위의 그림처럼 굵기가 변하는 관에 공기를 흐르게 하고 굵기가 다른 부분의 아래로 가는
유리관을 연결한다. 가는 유리관 속에서의 물의 높이를 관찰하면 굵은 쪽에 연결된 물기둥은
그 높이가 낮아지고, 가는 쪽에 연결된 물기둥은 높이가 높아진다. 같은 높이에서 유체가 흐르는
경우 유체의 속력은 좁은 통로를 흐를 때 증가하고 넓은 통로를 흐를 때 감소한다. 베르누이의 정리에
따르면 유체의 속력이 증가하면 유체 내부의 압력이 낮아지고, 반대로 속력이 감소하면 내부 압력이
높아진다. 압력이 높아지면 유리관 속의 물기둥을 더 세게 누르므로 물기둥의 높이가 낮아지고,
압력이 낮아지면 유리관 속의 물기둥을 약하게 누르므로 물기둥의 높이는 높아진다.
이 정리는 결국 이상유체에 대한 역학적 에너지 보존 법칙으로 생각할 수 있다.
그러나 이 법칙은 점성을 무시할 수 있는 완전유체가 규칙적으로 흐르는 경우에만 적용할 수 있고,
실제 유체에 대해서는 적당히 변형된다. 일반적으로 압류 시 유량계라고 하는 유량측정 장치는
이 원리를 이용한 것이다.
2. 층류와 난류
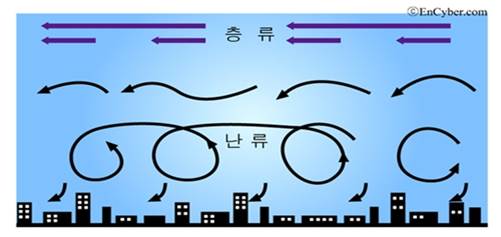
① 층류[層流, laminar flow]
유체의 규칙적인 흐름으로, 흐트러지지 않고 일정하게 흐르는 것을 말한다.
② 난류[亂流, turbulent flow]
유체역학에서 정의된 용어로, 유체의 각 부분이 시간적이나 공간적으로 불규칙한 운동을 하면서
흘러가는 것을 말한다.
3. 레이놀즈수
영국의 유체역학자 O. 레이놀즈가 발견하였다. 유체의 점성률(粘性率)을 점성계수를 , 밀도를 ,
유속 (流速)을 , 물체의 모양을 정하는 길이, 즉 구(球)나 원관(圓管)이면 반지름, 육 면 체면 변의
길이라 할 때, 무차원 수(無次元數)라 말한다.
4. 베르누이 방정식

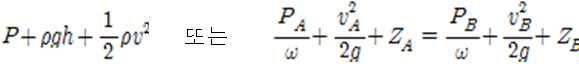
위의 그림처럼 베르누이 방정식은 유속 및 유량의 측정, 관로 유동해석 등 유체역학과 관련된 대부분의
문제를 해결하는 데 출발점이 되는 기본 방정식이다.
유체가 흐름선을 그리며 흐를 때, 두 점 A와 B의 높이 그리고 두 점에서의 압력과 흐르는 속도 사이의
관계를 두 점에서 역학적 에너지가 보존됨을 바탕으로 수식으로 나타낸 것을 가리킨다.
기준점에 대한 높이로 위치에너지를, 유체가 흐르는 속도로 운동에너지를, 압력으로 일(에너지) 을
나타낼 수 있는데 어느 한 점에서 이 세 에너지의 합은 다른 점에서의 세 에너지의 합과 같음을
나타내는 식이다.
이때 유체의 밀도는 변하지 않는다고 가정한다. 또 유체의 위치에너지나 운동에너지는 밀도를 써서
나타내어야 하며, 압력은 유체가 정지해 있을 때의 압력과 같지 않다.
이 관계식을 이용하여 흐르는 유체의 유속을 측정할 수 있다. 즉 흐르는 유체의 압력이 유체의 유속과
기준점에 대한 높이와 관계되기 때문이다. 송유관을 흐르는 기름의 속도, 비행기의 속도 등을 측정하는
데 응용된다.
'유체- 유공압류등' 카테고리의 다른 글
| 유량제어 밸브(Flow Control Valve) 회로의 종류 (0) | 2020.07.02 |
|---|---|
| 수격현상 (0) | 2020.07.01 |
| 공동현상(Cavitation) 과 서징 현상(Surging)이란 (0) | 2020.06.30 |
| 유압밸브 분류 (0) | 2020.06.15 |



