유한요소법
1) 유한요소법이란
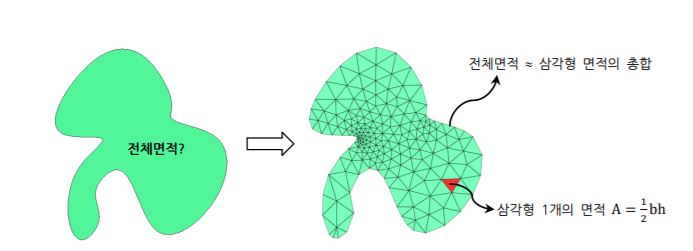
-공학과 수리 물리학 외 문제들을 풀기 위한 하나의 수치 기법
(1) 공학과 수리 물리학에서 유한요소법을 이용한 구조해석, 열전달, 유동장, 물질이동,
전자기장 해석을 통해 그 답을 구한다.
※두 개 이상의 요소들이 공유하는 점을 절점이라고 한다.
(2) 유한요소법은 전체 물체에 대한 문제를 한 번에 풀지 않고 각각의 유한 요소에 대해
방정식을 세우고 그들을 조합하여 전체에 대한 방정식을 구한다.
2) 일반적인 유한요소법
- 유한요소법은 일반적으로 유연 도법(하중법), 변위법(강성법)으로 구분된다.
(1) 유연 도법(강성법): 미지수로서 내력을 사용→ 지배 방정식을 구하기 위해 먼저 평형
방정식 사용→적합 방적식을 사용하여 필요한 방정식을 추가한다.
(2) 변위법(강성 법): 미지수로서 절점 변위 사용→ 하중에 작용하기 전에 공통 절점이나
공통 모서리, 공통 면에서 서로 연결되어 있다는 적합 조건을 우선
만족하며 평형 조건식과 힘과 변위를 연결하는 식을 이용하여 지배
방정식을 절점의 변위로 표현한다.
3) 유한요소법 수행 단계
(격자 분할과 요소 형태의 결정→ 변위 함수의 선정→ 변형률-변위와 응력-변형률 관계의
정의 → 요소 강성 행렬과 방정식의 유도→ 전체 행렬 구성 및 경계조건 적용→
미지의 자유도 풀기 → 요소 변형률과 응력 계산→ 결과 해석)
- 격자 분할과 요소 형태의 결정: 주어진 물체에서 사용될 전체 요소 수와 요소의 크기,
사용될 요소 형태를 공학자가 결정해야 할 주요
문제이다.
(작은 요소들은 일반적으로 기하학적 형상이 변하는 곳에서 필요
하고, 반면에 큰 요소들은 결과값이 상태적으로 일정한 부분에
사용함)

- 변위 함수의 선정: 각각의 요소 내에서의 변위 함수를 선택해야 하고 유한요소법에서는
변위와 같이 물체 내에서 연속된 물리량들이 이상모델로서 근사 되고
각각의 요소 내에서 정의된 구간별 연속함수들의 조합해야한다.
- 변형률-변위와 응력-변형률 관계의 정의: 재료 구성 법칙이라 불리며 응력-변형률 법칙을
통해 물체의 거동을 정확히 정의하는 능력으로
적합한 결과를 얻기 위해 가장 중요한 단계이다.
- 요소 강성 행렬과 방정식의 유도: 강성 행렬과 요소 방적식은 구조해석의 배경을 이루는
강성 영향 계수의 개념에서 시작됨

- 전체 행렬 구성 및 경계조건 적용: 전 단계에서 만든 개개의 요소 절점 평형 방정식을 전체
절점 평형 방정식으로 조합하는 단계이다.
-미지의 자유도에 대해 풀기: 유한요소법을 사용할 때 얻어지는 가장 처음의 값을 미지수라
말한다.

- 요소 변형률과 응력 계산: 구조 응력 해석 문제에 있어서 중요한 2차 물리량인 응력과
변형률을 구하는 단계이다.
- 결과 해석: 설계와 해석 과정에 응용하기 위해 결과를 이해하고 분석하는 단계이며 구조물
내의 대변형 이나 큰 응력이 발생한 위치를 알아내는 단계이다.

'유한요소-Abaqus,cad 등' 카테고리의 다른 글
| 유한요소법의 장점 (0) | 2020.07.29 |
|---|---|
| 유한요소법을 위한 컴퓨터 프로그램 (0) | 2020.07.27 |
| AutoCAD 기본 단축키 정리 (0) | 2020.05.24 |
| CAE 소프트웨어 Explicit , Implicit 비교 (0) | 2020.05.21 |


